Question

Answer in brief:

Explain what is meant by polarization and derive Malus’ law.

Answer 1

According to the electromagnetic theory of light, a light wave is made up of electric and magnetic fields that vibrate at right angles to each other and to the wave's propagation direction. 

If the vibrations of `vec"E"` in a light wave are perpendicular to the direction of light propagation, the wave is said to be unpolarized.

The electric field `vec "E"` in a light wave is said to be plane-polarized or linearly polarised if its vibrations are confined to a single plane containing the wave's propagation direction so that its electric field is restricted along one specific direction at right angles to the wave's propagation direction.

Polarization of light refers to the phenomenon of restricting the vibrations of light, i.e., the electric field vector, in a specific direction that is perpendicular to the direction of wave propagation.

Polarization of light

Consider an unpolarized light wave travelling along the x-direction. Let c, v and λ be the speed, frequency and wavelength, respectively, of the wave. The magnitude of its electric field `(vec"E")` is,

E = E₀ sin (kx - ωt), where E₀ = E_max = amplitude

of the wave, ω = 2πv = angular frequency of the wave and k = `(2pi)/lamda` = magnitude of the wave vector or propagation vector.

The intensity of the wave is proportional to `|"E"_0|^2`.

The direction of the electric field can be anywhere in the y-z plane. This wave is passed through two identical polarizers as shown in the following figure.

Unpolarized light passing through two identical polarizers

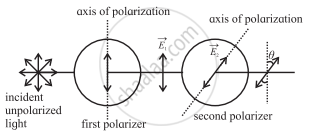
When a wave with an electric field inclined at an angle Φ to the first polarizer's axis passes through the polarizer, the component E0 cos Φ passes through it. The component E₀ sin Φ that is perpendicular to it will be blocked.

The intensity of this wave will now be proportional to the square of its amplitude after passing through this polarizer., i.e., proportional to `|"E"_0  "cos"  phi|^2`.

The intensity of the plane-polarized wave emerging from the first polarizer can be obtained by averaging `|"E"_0  "cos"  phi|^2` over all values of Φ between 0 and 180°. The intensity of the wave will be proportional to `1/2 |"E"_0|^2` as the average value of cos² Φ over this range is `1/2`. After passing through a polarizer, the intensity of an unpolarized wave is reduced by half.

When the plane-polarized wave emerges from the first polarizer, let us assume that its electric field `(vec"E"_1)` is along they-direction. In the above figure Thus, this electric field is

`vec"E"_1 = hat"j" "E"_10` sin (kx - ωt)       ....(1)

where E₁₀ is the amplitude of this polarized wave. The intensity of the polarized wave,

I₁ ∝ |E₁₀|²          .....(2)

Now, this wave passes through the second polarizer whose polarization axis (transmission axis) makes an angle θ with the y-direction. This allows only the component E₁₀ cos θ to pass through it. Thus, the amplitude of the wave which passes through the second polarizer is E₁₀ = E₁₀ cos θ and its intensity,

I₂ ∝ |E₂₀|²  

∴ I₂ ∝ |E₁₀|² cos² θ

∴ I₂ = I₁ cos² θ        ......(3)

Thus, when plane-polarized light of intensity I₁ is incident on the second identical polarizer, the intensity of light transmitted by the second polarizer varies as cos² θ, i.e., I₂ = I₁ cos² θ, where θ is the angle between the transmission axes of the two polarizers. This is known as Malus' law.