Question

Answer the following :

Find the lengths of the intercepts made on the co-ordinate axes, by the circle:

x² + y² – 5x + 13y – 14 = 0

Answer 1

To find x-intercept made by the circle x² + y² + 2gx + 2fy + c = 0, substitute y = 0 and get a quadratic equation in x, whose roots are, say, x₁ and x₂

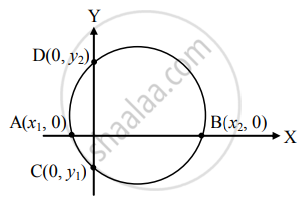
These values represent the abscissae of ends A and B of x – intercept.

Length of x – intercept = |AB| = |x₂ – x₁| Similarly, substituting x = 0, we get a quadratic equation in y whose roots, say, y₁ and y₂ are ordinates of the ends C and D of y-intercept. Length of y – intercept = |CD| = |y₂ – y₁|

Given equation of the circle is

x² + y² – 5x + 13y – 14 = 0    …(i)

Substituting y = 0 in (i), we get

x² – 5x – 14 = 0      …(ii)

Let AB represent the x-intercept, where

A = (x₁, 0), B = (x₂, 0).

Then from (ii),

x₁ + x₂ = 5 and x₁x₂ = – 14

(x₁ – x₂)² = (x₁ + x₂)² – 4 x₁x₂

= (5)² – 4(– 14)

= 25 + 56

= 81

∴  |x₁ – x₂| = `sqrt((x_1 - x_2)^2) = sqrt(81)` = 9

∴ Length of x-intercept = 9 units

Substituting x = 0 in (i), we get

y² + 13y – 14 = 0      …(iii)

Let CD represent the y-intercept, where

C = (0, y₁), D = (0, y₂).

Then from (iii),

y₁ + y₂ = – 13 and y₁ y₂ = – 14

(y₁ – y₂)² = (y₁ + y₂)² – 4 y₁ y₂

= (– 13)² – 4(– 14)

= 169 + 56

= 225

∴ |y₁ – y₂| = `sqrt((y_1 - y_2)^2) = sqrt(225)` = 15

∴ Length of y-intercept = 15 units