Question

Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is ______.

Options

• 3(π – 2)

• 6(π – 2)

• 6(4 – π)

• 3(4 – π)

Answer 1

Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is 6(π – 2).

Explanation:

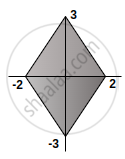
`|x|/2 + |y|/3` = 1 outside

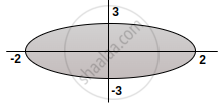
`x^2/4 + y^2/9` = 1 inside

`|x|/2 + |y|/3 = 1 = {{:(x/2 + y/3 = 1",", x > 0, y > 0),((-x)/2 + y/3 = 1, x < 0, y > 0),(- x/2 - y/2 = 1, x < 0, y < 0),(x/2 - y/3 = 1, x > 0, y < 0):}`

`x^2/4 + y^2/9` = 1 ellipse

Combined graph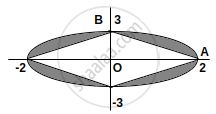
  Area of the shaded portion

Area of ellipse πab = π × 2 × 3 = 6π

Area of ΔOAB = `1/2 xx 2 xx 3` = 3

So area of shaded part in first quadrant = `1/4(6π) - 3 = 3/2π - 3`

Area of whole curve = `4(3/2π - 3)`

= 6π – 12

= 6(π – 2)