Question

Area lying in the first quadrant and bounded by the circle `x^2 + y^2 = 4` and the lines `x + 0` and `x = 2`.

Options

• `pi`

• `pi/2`

• `pi/3`

• `pi/4`

Answer 1

`pi`

Explanation:

A circle of radius '2' is drawn

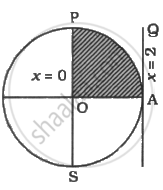
The line OP is `x` = 0

And AQ it `x` = 2

∴ Area 'A' of the required region OAP = `int_0^2 y  dx`

Equation of the circle is `x^2 + y^2` = 4

∴ `y^2 = 4 - x^2` or `y = sqrt(4 - x^2)`

A = `int_0^2 sqrt(4 - x^2)  dx [x/2 sqrt(4 - x^2) + 4/2 sin^-1  x/2]_0^2`

`[because  int sqrt(a^2 - x^2)  dx = (xsqrt(a^2 - a^2))/2 + a^2/2 sin^-1  x/a  "here"  a = 2]`

∴ A = `[0 + 2 sin^-1  2/2] = 2 sin^-1 = 2 xx pi/2` = π.