Question

Area of the equilateral triangle inscribed in the circle x² + y² – 7x + 9y + 5 = 0 is ______.

Options

• `155/8 sqrt(3)` square units

• `168/8 sqrt(3)` square units

• `175/8 sqrt(3)` square units

• `165/8 sqrt(3)` square units

Answer 1

Area of the equilateral triangle inscribed in the circle x² + y² – 7x + 9y + 5 = 0 is `underlinebb(165/8 sqrt(3)  "square units")`.

Explanation:

Given circle : x² + y² – 7x + 9y + 5 = 0

∴ Centre = `(7/2, (-9)/2)`

Radius = `sqrt(49/4 + 81/4 - 5)`

= `sqrt(110)/2`

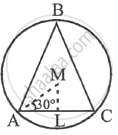
Since, ΔABC is an equilateral

∴ ∠MAL = 30°, ∠MLA = 90°

Also MA = `sqrt(110)/2`

 ∴ AL = MA cos 30° = `sqrt(110)/2 xx sqrt(3)/2 = sqrt(330)/4`

∴ Side of Δ = 2.AL = `sqrt(330)/2`

Area of equilateral Δ = `sqrt(3)/4 a^2 = sqrt(3)/4 xx 330/4`

= `165/8 sqrt(3)` sq.units