Question

Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is

Options

• 8 sq units

• 16 sq units

• 32 sq units

• None of these

Answer 1

16 sq units

Explanation:

Given equation of the curves are

y = |x + 1| + 1 = `{{:((x + 1) + 1",",  "If"  x + 1 ≥ 0),(-(x + 1) + 1",",  "If" x + 1 < 0):}`

= `{{:(x + 2",",  "if"  x ≥  - 1),(-x",",  "if"  x < - 1):}`  ......(i)

x = – 3  ......(ii)

x = 3  ......(iii)

and y = 0  ......(iv)

Equation (ii) represents the line parallel to y-axis and passes through the point (–3, 0).

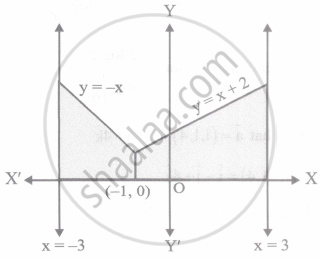
Equation (iii) represents the line parallel to y-axis and passes through the point (3, 0).

∴ Required area = `int_(-3)^(-1) y  dx + int_(-1)^3  y  dx`

= `int_(-3)^(-1) - x  dx + int_(-1)^3  (x + 2)  dx`

= `[(-x^2)/2]_(-3)^(-1) + [x^2/2 + 2x]_(-1)^3`

= 16 sq.units