Advertisements
Advertisements
Question
By the graphical method, find whether the following pair of equations are consistent or not. If consistent, solve them.
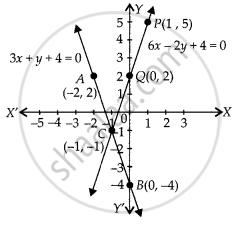
3x + y + 4 = 0, 6x – 2y + 4 = 0
Solution
Given pair of equations are
3x + y + 4 = 0 ......(i)
And 6x – 2y + 4 = 0 .......(ii)
On comparing with ax + by + c = 0, we get
a1 = 3, b1 = 1 and c1 = 4 ......[From, (i)]
a2 = 6, b2 = –2 and c2 = 4 ......[From (ii)]
Here, `a_1/a_2 = 3/6 = 1/2`;
`b_1/b_2 = 1/(-2)`
And `c_1/c_2 = 4/4 = 1/1`
∵ `a_1/a_2 ≠ b_1/b_2`
So, the given pair of linear equations are intersecting at one point,
Therefore these lines have unique solution.
Hence, given pair of linear equations are consistent.
We have, 3x + y + 4 = 0
⇒ y = – 4 – 3x
We have, 3x + y + 4 = 0
⇒ y = – 4 – 3x
| x | 0 | – 1 | – 2 |
| y | – 4 | – 1 | 2 |
And 6x – 2y + 4 = 0
⇒ 2y = 6x + 4
⇒ y = 3x + 2
| x | – 1 | 0 | 1 |
| y | – 1 | 2 | 5 |
Plotting the points B(0, – 4) and A(– 2, 2), we get the straight line AB,
Plotting the points Q(0, 2) and P(1, 5), we get the straight line PQ.
The lines AB and PQ intersect at C(– 1, – 1).