Question

Calculate packing efficiency in face-centred cubic lattice.

Answer 1

Step 1: Radius of sphere:

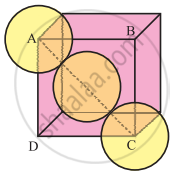
In the unit cell of face-centred cubic lattice, there 8 atoms at 8 corners and 6 atoms at 6 face centres.

Consider the face ABCD.

The atoms are in contact along the face diagonal BD. Let a be the edge length and r, the radius of an atom.

Consider a triangle BCD.

BD² = BC² + CD²

= a² + a² = 2a²

`∴ "BD" = sqrt2 a`

From figure, BD = 4r

`∴ 4r = sqrt2a and r - sqrt2/4a = a/(2sqrt2)`

Step 2: Volume of sphere:

`"Volume of one particle" = 4/3 πr^3`

`= (4π)/3 xx (a/(2sqrt2))^3`

`= 4/3πa^3(1/(2sqrt2))^3`

`= (πa^3)/(12sqrt2)`

`"total volume of 4 particles in unit cell" =  4 xx (πa^3)/(12sqrt2) = (πa^3)/(3sqrt2)`

Step 3: Packing efficiency:

`"Packing efficiency" = ("Volume occupied by particles in unit cell")/("Volume of unit cell")xx 100`

`= ((πa^3)/(3sqrt2))/a^3 xx 100`

`= (3.142)/(3sqrt2) xx 100 = 74%`