Advertisements
Advertisements
Question
चाँदे की सहायता से 110° का एक कोण खींचिए और फिर इसे समद्विभाजित कीजिए। प्रत्येक कोण को मापिए।
Advertisements
Solution
चाँदे की सहायता से ∠BXA = 110° खींचिए।
अब, हम आवश्यक निर्माण के लिए निम्नलिखित चरणों का उपयोग करते हैं।
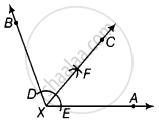
1. X को केंद्र मानकर और कोई त्रिज्या लेकर एक चाप खींचिए जो किरणों XA और XB को क्रमश : E और D पर प्रतिच्छेद करे।
2. D और E को केंद्र मानकर और `1/2` DE से अधिक त्रिज्या लेकर, प्रतिच्छेद करने के लिए चाप लगाइए। एक दूसरे को, F पर कहते हैं।
3. किरण XF खींचिए। इस प्रकार, किरण XF कोण BXA की अभीष्ट समद्विभाजक है। प्रत्येक कोण को मापने पर, हम पाते हैं।
∠BXC = ∠AXC = 55° ...[∴ ∠BXC = ∠AXC = `1/2` ∠BXA = `1/2` × 110° = 55°]
APPEARS IN
RELATED QUESTIONS
एक दी हुई किरण के प्रारंभिक बिंदु पर 90° का कोण रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।
एक दी हुई किरण के प्रारंभिक बिंदु पर 45° के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।
75° के कोणों की रचना कीजिए और इसे एक चांदे से मापकर सत्यापित कीजिए।
135° के कोणों की रचना कीजिए और इसे एक चांदे से मापकर पुष्टि कीजिए।
एक समबाहु त्रिभुज की रचना कीजिए, जब इसकी भुजा दी हो तथा कारण सहित रचना कीजिए।
पटरी और परकार की सहायता से निम्नलिखित कोण की रचना करना संभव नहीं है :
एक त्रिभुज ABC, जिसमें BC = 3 cm और ∠C = 60° है, की रचना संभव है जब AB और AC अंतर बराबर है :
4 cm लंबाई का एक रेखाखंड खींचिए। क्रमश : A और B से होकर, AB पर लंब रेखाएँ खींचिए। क्या ये रेखाएँ समांतर हैं?
चाँदे की सहायता से 80° का एक कोण खींचिए। 40°, 160° और 120° के कोणों की रचना कीजिए।
एक समचतुर्भुज की रचना कीजिए, जिसकी एक भुजा 3.4 cm है और जिसका एक कोण 45° का है।
