Question

Change the order of integration and evaluate `int_0^2 int_(2-sqrt(4-y^2))^(2+sqrt(4-y^2)) dxdy` 

 

Answer 1

1) Given order and given limits: Given order is is: first w.r.t. x and then w.r.t y i.e., a strip parallel to the x-axis varies from `x=2-sqrt(4-y^2)` to `x=2- sqrt(4-y^2).y ` varies from y = 0 to y = 2. 

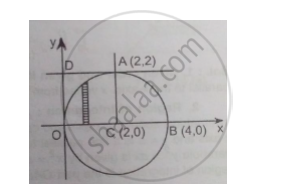
2) Region of integration: `x=2-sqrt(4-y^2)` is the arc and `x =2+sqrt(4-y^2)` is the arc of the circle` (x-2)^2+y^2=4` 4with centre at (2, 0) and radius = 2 above the x-axis. y = 0 is the x-axis and y = 2 is the line parallel to the x-axis through A (2, 2). The region of integration is the semi-circle OAB above the x-axis. The points of intersection of the circle and the x-axis are O (0, 0) and B (4, 0). 

3) Change of order of integration: To change the order, consider a strip parallel to the y-axis in the region of integration. On this strip y varies from y = 0 to y=`sqrt4-(x-2)^2` and then strip moves from x = 0 to x = 4  

`I= int_0^4 int_0^sqrt(4-(x-2)^2) dydx` 

`I=int_0^4 [y]_0^sqrt(4-(x-2)^2 dx)` 

`I=int_0^4 sqrt(4-(x-2)^2) dx` 

`I=[x-2/2 sqrt(4-(x-2)^2)+2sin ^ -1  (x-2)/2]_0^4` 

`I= (2.pi/2)-(-2. pi/2)` 

∴` I=2pi`