Question

Choose the correct answer:

A parallel-plate capacitor has circular plates of radius 8 cm and plate separation I mm. What will be the charge on the plates if a potential difference of 100 V is applied across its plates?

Options

• 1.78 × 10^-8C

• 1.78 × 10^-5C

• 4.3 × 10⁴C

• 2 × 10^-9C

Answer 1

1.78 × 10^-8C

Explanation:

The capacitance of a parallel plate capacitor is given as follows:

C = `(ε_0A)/d`

Here, ε₀ is the permittivity of free space, A is the plate area, and d is the separation between the plates.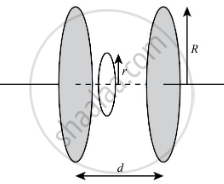

For circular plates as shown in the above figure, the area of the plates can be calculated as follows:

A = `piR^2`

Therefore the capacitance can be expressed as:

C = `(ε_0 piR^2)/d`  .....(1)

Substitute 8 cm for R, 1 mm for d, and `8.85 xx 10^-12 CV^-1 m^-1` for ε₀ in equation (1) to find the value of C.

C = `((8.85 xx 10^-12 CV^-1 m^-1)*(3.14)*(8 xx 10^-2 m^2)^2)/(1 xx 10^-3 m)`

C = `1.78 xx 10^-10 CV^-1`

The charge on the capacitor is given as follows:

Q = CV  .....(2)

Substitute 100V for V and `1.78 xx 10^-10 CV^-1` for C in equation (2) to find the value of Q.

Q = `(1.78 xx 10^-10 CV^-1) * (100V)`

Q = `1.78 xx 10^-8 C`