Advertisements
Advertisements
Question
Solution
g1 = 9.8 ms−2
g2 = 4.36 ms−2
Now, time period of pendulum is, `"T" = 2root(pi)(l/g)`
`"T"_1 = 2root(pi)(l/(g_1))`
`"T"_1 = 2root(pi)(l/9.8)`
= 2π × 0.3194 × 1 = 2.0061
Similarly,
`"T"_2 = 2root(pi)(l/(g_2))`
`"T"_2 = 2root(pi)(l/(4.36))`
= 2π × 0.4789 × 1 = 3.0071
T1 : T2 = 2.0061 : 3.0071
= 0.667 : 1
APPEARS IN
RELATED QUESTIONS
The distance of a galaxy is 5·6 × 1025 m . Assuming the speed of light to be 3 × 108 `"ms"^-1`. Find the time taken by light to travel this distance .
[Hint : `"Time taken" = "Distance travelled"/"speed"`]
Define simple pendulum.
Write an expression for the time period of a simple pendulum.
Which of the following do not affect the time period of a simple pendulum?
- mass of bob
- size of bob
- effective length of pendulum
- acceleration due to gravity
- amplitude.
Draw a graph of l, the length of simple pendulum against T2, the square of its time period.
What is a best fit line for a graph?
What does the best fit line show regarding the variables plotted and the work of the experimenter?
What do you understand by the term constant of proportionality?
Define the following terms with reference to a simple pendulum:
Frequency
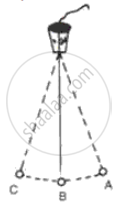
If a pendulum takes 0.5 s to travel from A to B as shown in the following figure, find its time period and frequency.