Question

Consider a 20 kg uniform circular disk of radius 0.2 m. It is pin supported at its center and is at rest initially. The disk is acted upon by a constant force F = 20 N through a massless string wrapped around its periphery as shown in the figure.

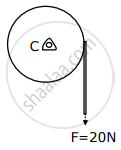
Suppose the disk makes n number of revolutions to attain an angular speed of 50 rad s^–1. The value of n, to the nearest integer, is ________.

In one complete revolution, the disk rotates by 6.28 rad.

Options

• 20

• 25

• 35

• 30

Answer 1

20

Explanation:

Mass of a disk = 20 kg

The radius of a disk = 0.2 m

Torque due to force, F = 20 N is τ.

Since,  τ = I α

F = `"mr"^2/2alpha`

α = `(2"F")/("mr") = (2xx20)/(20xx0.2)` ⇒ 10 rad/s²

Using the kinematic equation for rotational motion,

ω² = `ω_0^2` + 2α θ

(50)² = 0 + 2(10) θ

θ = `2500/20` = 125 radian

No. of revolution `125/6.28` ≈ 20 revolution