Question

Consider a badminton racket with length scales as shown in the figure.

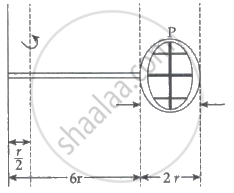
If the mass of the linear and circular portions of the badminton racket is the same (M) and the mass of the threads is negligible, the moment of inertia of the racket about an axis perpendicular to the handle and in the plane of the ring at, `r/2` distance from the ends A of the handle will be ______ Mr².

Options

• 50

• 51

• 52

• 55

Answer 1

52 Mr²

Explanation:

In this,

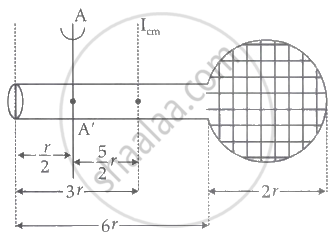
In order to obtain the moment of inertia of the linear and circular components of the issue, we must apply the parallel axis theorem twice.

MI of linear part,

`I_(A A)^' = I_{cm} + Md^2`

= `(M(6r)^2)/12 + M(5/2 r)^2`

`I_(A A)^' = (36Mr^2)/12 + (25Mr^2)/4`

MI of circular part,

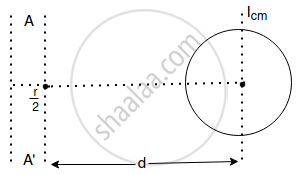
`I_(A A)^' = I_{cm} + Md^2`

= `(Mr^2)/2 + M(13/2 r)^2`

`I_(A A)^' = (Mr^2)/2 + 169/4 Mr^2`

Net M.I	=	IAA	+	IAA
		↓		↓
		Linear part		Circular part

Net MI = `((36Mr^2)/12 + 25/4 Mr^2) + ((Mr^2)/2 + 169/4 Mr^2)`

Net MI = 52 Mr²