Advertisements
Advertisements
Question
Consider a particle of mass m suspended by a string at the equator. Let R and M denote radius and mass of the earth. If ω is the angular velocity of rotation of the earth about its own axis, then the tension on the string will be (cos 0° = 1).
Options
`"GMm"/"R"^2`
`"GMm"/"2R"^2`
`"GMm"/"2R"^2 + "m" omega^2 "R"`
`"GMm"/"R"^2 - "m" omega^2 "R"`
Solution
`"GMm"/"R"^2 - "m" omega^2 "R"`
Explanation:
When a body suspended by the string situated at position Pas shown in the figure, where latitude is λ, then body is also rotated with angular frequency (ω) of earth, hence tension on the string is given by
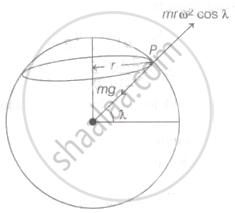
T = mg - mrω2 cos λ
T = `"m" * "GM"/"R"^2 - "mr"omega^2 cos lambda ...[therefore "g" = "GM"/"R"^2]`
T = `"GMm"/"R"^2 - "mr"omega^2 cos lambda` ....(i)
When body is suspended at equator, then
λ = 0 and r = R
∴ From Eq. (i), we have,
T = `"GMm"/"R"^2 - "mR"omega^2 cos 0^circ`
T = `"GMm"/"R"^2 - "mR"omega^2`
