Question

Consider the two sets : A = {m ∈ R : both the roots of x² – (m + 1)x + m + 4 = 0 are real} and B = [–3, 5). Which of the following is not true?

Options

• A – B = (–∞, –3) ∪ [5, ∞)

• A ∩ B = {–3}

• B – A = (–3, 5)

• A ∪ B = R

Answer 1

A – B = (–∞, –3) ∪ [5, ∞)

Explanation:

A = {m ∈ R : x² – (m + 1)x + m + 4 = 0 has real roots}

D ≥ 0

⇒ (m + 1)² – 4(m + 4) ≥ 0

⇒ m² – 2m – 15 ≥ 0

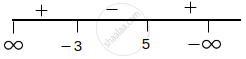
A = {(–∞, –3] ∪ [5, ∞)}

B = [–3, 5)

⇒ A – B = (–∞, –3) ∪ [5, ∞)