Question

Construct ΔABC, in which BC = 3.2 cm, ∠ACB = 45° and perimeter of ΔABC is 10 cm.

Answer 1

Rough figure:

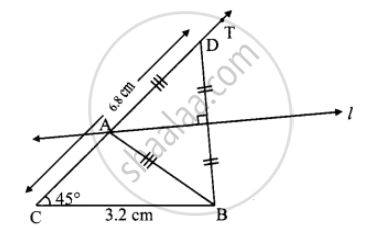
Explanation:

Perimeter of Δ ABC = 10 cm

⇒ AB + BC + AC = 10 cm

⇒ AB + 3.2 + AC = 10 cm

⇒ AB + AC = 6.8 cm

Now, In ∆ABC

BC = 3.2 cm, ∠ACB = 45° and AB + AC = 6.8 cm    ...(i)

As shown in the rough figure draw seg BC = 3.2 cm

Draw a ray CT making an angle of 45° with CB

Take a point D on ray CT, such that

CD = 6.8 cm

Now, CA + AD = CD     ...[C-A-D]

∴ CA + AD = 6.8 cm       ...(ii)

Also, AB + AC = 6.8 cm     ...(iii) [From (i)]

∴ CA + AD = AB + AC      ...[From (ii) and (iii)]

∴ AD = AB

∴ Point A is on the perpendicular bisector of seg DB.

∴ The point of intersection of ray CT and perpendicular bisector of seg DB is point A.

Steps of construction:

1. Draw seg BC of length 3.2 cm.
2. Draw ray CT, such that ∠BCT = 45°.
3. Mark point D on ray CT such l(CD) = 6.8 cm.
4. Join points D and B.
5. Draw perpendicular bisector of seg DB intersecting ray CT. Name the point as A.
6. Join the points A and B.

Therefore, ∆ABC is the required triangle.