Question

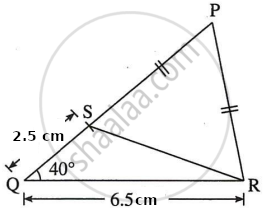
Construct ΔPQR, such that QR = 6.5 cm, ∠PQR = 40° and PQ - PR = 2.5 cm.

Answer 1

Rough figure:

Explanation:

Here, PQ – PR = 2.5 cm

∴ PQ > PR

As shown in the rough figure draw seg QR = 6.5 cm

Draw a ray QX making on angle of 40° with QR

Take a point S on ray QX, such that QS = 2.5 cm

Now, PQ – PS = QS     ...[Q-S-T]

∴ PQ – PS = 2.5 cm    ...(i) [Given]

Also, PQ – PR = 2.5 cm    ...(ii) [From (i) and (ii)]

∴ PQ – PS = PQ – PR

∴ PS = PR

∴ Point P is on the perpendicular bisector of seg RS.

∴ Point P is the intersection of ray QX and the perpendicular bisector of seg RS

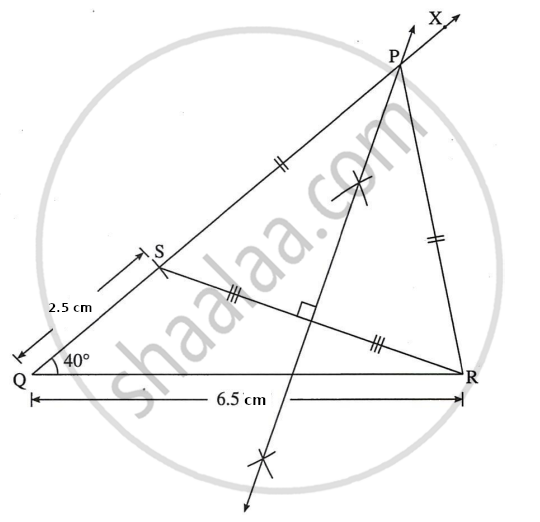
Steps of construction:

1. Draw seg QR of length 6.5 cm.
2. Draw ray QX such that ∠RQX = 40°
3. Take point S on ray QX such that QS = 2.5 cm.
4. Join points S and R.
5. Draw perpendicular bisector of seg SR intersecting ray QX. Name the point as P.
6. Draw seg PR.

 Therefore, ΔPQR is required triangle.