Question

Derive an expression for the electric potential at a point due to a short electric dipole. Hence, write the expression for the electric potential at a point (i) dipole axis and (ii) on the dipole equator.

Answer 1

Think about an electric dipole AB with point charges + q and − q, and a dipole length of 2l. The magnitude of its electric dipole moment, `vecp`, is p = 2ql. As seen in the picture, P is a point located r away from O, the dipole's centre, in a direction θ perpendicular to the dipole axis. Assume BP = r₂ and AP = r₁.

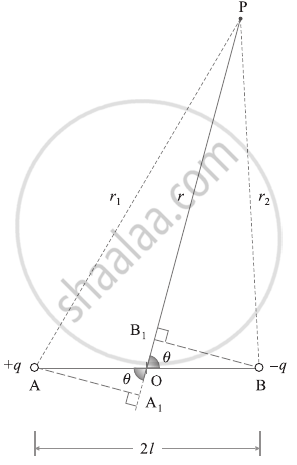
Electric potential due to a short electric dipole

The electric potential at P due to the charge + q is

`V_1 = + 1/(4πε_0) q/r_1`   ... (1)

and that due to the charge − q is

`V_2 = + 1/(4πε_0) q/r_2`   ... (2)

Since the potential is a scalar quantity, the resultant electric potential at P due to the dipole is

V = V₁ + V₂

= `1/(4πε_0) q/r_1 - 1/(4πε_0) q/r_2`

= `q/(4πε_0) (1/r_1 - 1/r_2)`   ... (3)

From Δ PAA₁, by the cosine rule,

`r_1^2` =  r² + l² + 2rl cos (180° − θ)

= `r^2 (1 + l^2/r^2 - 2 l/r cos θ)`

≃ `r^2 (1 - 2l/r cos θ)`

When `l^2/r^2` has been ignored because, for a short dipole (2l ≪ r), so that `l/r ≪ 1`.

∴ `r_1 = r (1 - 2 l/r cos θ)^(1/2)`

∴ `1/r_1 = 1/r (1 - 2 l/r cos θ)^(- 1/2) ≃ 1/r (1 + l/r cos θ)`

ignoring higher powers of `l/r` in the binomial expansion.

Similarly, `r_2^2 ≃ r^2 (1 + 2 l/r cos θ)`

∴ `r_2 = r (1 + 2 l/r cos θ)^(1/2)`

∴ `1/r_2 = 1/r (1 + 2 l/r cos θ)^(- 1/2) ≃ 1/r (1 - l/r cos θ)`

∴ `1/r_1 - 1/r_2 = 1/r ((2l)/r cos θ) = (2l)/r^2 cos θ`    ... (4)

∴ From Eqs. (3) and (4).

V = `q/(4πε_0) ((2l cos θ)/r^2) = 1/(4πε_0). ((2ql)cos θ)/r^2`   ... (5)

= `1/(4πε_0) (p cos θ)/r^2`   ... (6)

This is the required expression.

(i) At a point on the dipole axis, θ 0° (nearer to the charge + q) or 180° (nearer to the charge − q).

∴ cos θ = ± 1

∴ V_axis = `± 1/(4πε_0). p/r^2`

(ii) At a point on the dipole equator, θ 90° or 270° (equidistant from both the charges).

∴ cos θ = 0   ∴ V_equator = 0