Question

Derive an expression for the electric potential energy of an electric dipole in a uniform electric field.

Answer 1

Think about an electric dipole with a dipole moment of `vecp` that is positioned at an angle ∅ with `vecE` in a uniform electric field `vecE`. The dipole rotates and aligns with `vecE` with the torque `vecτ` = `vecp` × `vecE`.

Assume that an external torque `vecτ_(ext)`, which is applied to spin the dipole through a minuscule angular displacement d∅ while maintaining equilibrium, is applied. The torque should be equal in magnitude and opposite in direction to `vecτ`.

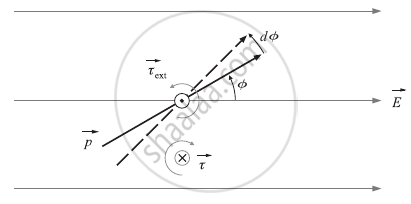
Rotating an electric dipole in an external electric field

The work done by this torque is

dW = τ_ext d∅ = pE sin ∅ d∅

In a finite angular displacement from θ₀ to θ, the total work done on the dipole by the external agent is

W = `intdW = int_(θ_0)^θ pE sin ∅ d∅`

= `pE int_(θ_0)^θ sin ∅ d∅`

= `pE [− cos ∅]_(θ_0)^θ`

= − pE (cos θ − cos θ₀)   ... (1)

= pE (cos θ₀ − cos θ)

If the dipole was initially parallel to `vecE`, θ₀ = 0 and cos θ₀ = 1.

∴ W = pE (1 − cos θ)   ... (2)

The dipole's potential energy, U₀ = − pE, is the smallest (more negative) if it was initially parallel to `vecE`. Should we arbitrarily designate U₀ = 0 as the minimal potential energy, then the system's potential energy with an inclination of θ is

U_θ = − pE cos θ = `-vecp`. `vecE`

This is the required expression.