Question

Derive an expression for the emf induced in a straight conductor moving in a uniform magnetic field with constant velocity.

Answer 1

Imagine a straight wire AB that is completely in a plane perpendicular to a uniform magnetic field `vecB`, resting on two conducting rails that are spaced apart by a distance l. The rails are fixed with respect to the field and linked to a stationary resistor R, and `vecB` is pointing into the page.

Assume that the rod is moved to the right by an outside force at a constant speed v that is both perpendicular to its length and to lB. The area of the loop ABCD grows by dA = ldx = lvdt as the rod travels over a distance dx = vdt in time dt.

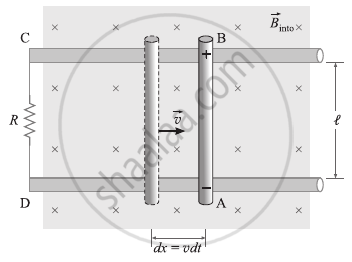
A conducting rod is moved to the right on conducting rails in a uniform magnetic field

Therefore, in time dt, the increase in the magnetic flux through the loop,

dΦ_m = BdA = Blvdt

By Faraday’s law of electromagnetic induction, the magnitude of the induced emf

`e = (dΦ_m)/dt = (Blvdt)/dt = Blv`