Question

Derive an expression for the impedance of an LCR circuit connected to an AC power supply. Draw phasor diagram.

Answer 1

Now let us consider the total opposition offered by a resistor, pure inductor, and capacitor connected in series with the alternating source of emf,

Series LCR circuit

Let a pure resistor R, a pure inductance L, and an ideal capacitor of capactance C be connected in series to a source of alternative emf. As R, L and C are in series, the current at any instant through the three elements has the same amplitude and phase. Let it be represented by

i = i₀ sin ωt.

The voltage across each element bears a different phase relationship with the current. The voltages e_L, e_C and e_R are given by

e_R = iR, e_L = iX_L and e_C = iX_C

As the voltage across the capacitor lags behind the alternating current by 90°, it is represented by `bar(OC)`, rotated clockwise through 90 from the direction of `bar(i_0)`. `bar(OC)` is along OY' in the phasor diagram shown in the phasor diagrams in Fig. of the phasor diagram.

As eR is in phase with current i₀, the vector eR is drawn in the same direction as that of i, along the positive direction of the X-axis represented by `bar(OA)`. The voltage across L and C have a phase different of 180°; hence, the net reactive voltage is (e_L− e_C).

Assuming e_L> e_C represented by OB' in the figure.

The resultant of `bar(OA) and bar(OB)"'"` is the diagonal OK of the rectangle OAKB'.

`therefore OK = sqrt(OA^2 + OB^2)`

`e_0 = sqrt(e_R^2 + (e_L - e_C)^2)`

= `sqrt((i_0R)^2 + (i_0X_L - i_0X_C)^2`

`e_0 = i_0sqrt(R^2 + (X_L - X_C)^2`

`therefore e_0/i_0 = sqrt(R^2 + (X_L - X_C)^2`

`e_0/i_0 = Z`

Comparing the above equation with the relation `V/i = R`, the quantity `sqrt(R^2 + (X_L - _C)` represents the effective opposition offered by the inductor, capacitor, and resistor connected in series to the flow of AC current. This total effective resistance of the LCR circuit is called the impedance of the circuit and is represented by Z. The reciprocal of the impedance of an AC circuit is called admittance. Its SI unit is ohm⁻¹ or Siemens.

It can be defined as the ratio of rms voltage to the rms value of current Impedance is expressed in ohm (Ω).c

Phasor diagram:

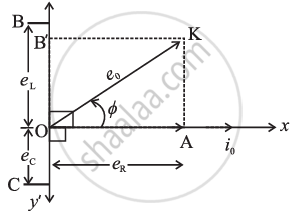
From the phasor diagram, it can be seen that in an AC circuit containing L, C and R, the voltage leads the current by a phase angle Φ.

`tan phi = (AK)/(OA) = (OB"'")/(OA) = (e_L - e_C)/e_R = (i_0X_L - i_0X_C)/(i_0R)`

`tan phi = (X_L -X_C)/R`

`therefore phi = tan^-1((X_L - X_C)/L)`

∴ The alternating current in LCR circuit would be represented by

i = i₀ sin (ωt + Φ)

and e = e₀ sin (ωt + Φ)