Advertisements
Advertisements
Question
Derive the conditions of maxima and minima due to interference of light reflected from thin film of uniform thickness.
Solution
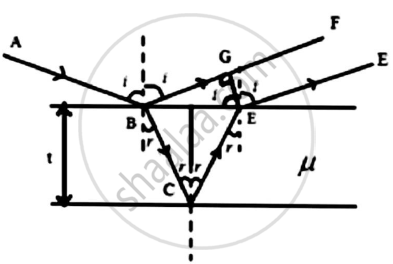
Consider a thin film of uniform thickness (t) and R.I (μ)
On Reflected side,
The ray of light BF and DE will interfere.
The path difference between BF and DE is,
Δ = μ(BC + CD) − BG
`BC = CD = t/cosr`..........(1)
Now,
BD = (2t) tan r .......(2)
BG = BD sin i
BG = (2t) tan r sin i
`BG = 2tμsinr(sinr / cosr)`
`BG = 2μt(sin^2r/cosr)`..........(3)
Substituting (i) and (iii) in Δ :
`Δ = μ(t / cosr + t / cosr)−2μt(sin^2r / cosr)`
= 2μtcosr(1−sin2r)
Δ = 2μtcosr
This is a geometric path difference. However, there is a phase change of π, as ray BF is reflected from a denser medium. Hence we need to add ±λ2 to path difference
Δ = 2μtcosr ± λ2
For Destructive Interference:
Δ = nλ
2μtcosr±λ2=nλ
`2μtcosr=(2n±1)λ2.....(n=0,1,2,...)`
This is the required expression for constructive Interference or Maxima.
For Destructive interference:
`Δ = (2n±1)λ/2`
`2μtcosr ± λ/2 = nλ`
2μtcosr = nλ
This is the required expression for destructive interference
.
APPEARS IN
RELATED QUESTIONS
Obtain the condition for maxima and minima of the light reflected from a thin transparent film of uniform thickness. Why is the visibility of the fringe much higher in the reflected system than in the transmitted system.
What is meant by thin film? Comment on the colours in thin film in sunlight.
Derive the conditions of maxima and minima due to interference of light transmitted from thin film of uniform thickness.
What is antireflection coating? What should be the refractive index and minimum thickness of the coating?
