Advertisements
Advertisements
Question
Derive expression for gravitational potential energy for a body placed at a height above the ground.
Solution
Derivation of Expression [U = mgh].
Assume that a mass m body is raised to a vertical height h from the earth's surface.
Without acceleration, the force (mg) needed to raise the body is equal to the force of gravity pulling it down vertically.
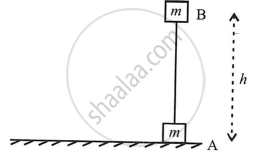
Work done to lift body from A to B
W = Force of gravity × Displacement above the ground
= mg × h
W = mgh
This work is stored as gravitational potential energy within the body.
RELATED QUESTIONS
A metallic ball is hanging by a string from a fixed support. Draw a neat labelled diagram showing the forces acting on the ball and the string.
What is meant by the gravitational potential energy?
Two bodies of equal masses are placed at heights h and 2h. Find the ratio of their gravitational potential energies.
Find the gravitational potential energy of 1 kg mass kept at a height of 5 m above the ground. Calculate its kinetic energy when it falls and hits the ground. Take g = 10 m s-2.
Calculate the height through which a body of mass 0.5 kg is lifted if the energy spent in doing so is 1.0 J. Take g = 10 m s-2.
A man of mass 50 kg climbs up a ladder of height 15 m. Calculate:
- the work done by the man,
- the increase in his potential energy. (g = 9.8 m s-2)
The diagram given below shows a ski jump. A skier weighing 60 kgf stands at A at the top of ski jump. He moves from A and takes off for his jump at B.

- Calculate the change in the gravitational potential energy of the skier between A and B.
- If 75% of the energy in part
- becomes kinetic energy at B.
- Calculate the speed at which the skier arrives at B. (Take g = 10 m s-2)
Draw a graph of potential energy vs height for a body thrown vertically upwards. [Assume no friction is present.]
Write an expression for the potential energy of a body of mass m placed at a height h above the earth's surface. State the assumptions made, if any.
A box of mass 300 kg has gravitational potential energy stored in it equal to 29400 J. Find the height of the box above the ground. (Take g = 9·8 N kg-1).
