Question

Derive the equation for effective focal length for lenses in out of contact.

Answer 1

1. Let O be a point object on the principal axis of a lens. OA is the incident ray on the lens at a point A at a height h above the optical centre. The ray is deviated through an angle δ and forms the image I on the principle axis.
2. The incident and refracted rays subtend the angles. ∠ AOP = α and ∠ AIP = β with the principle axis respectively.
   
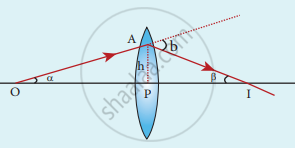
3. In the triangle ∆ OAI, the angle of deviation δ can be δ = α + β
   If the height h is small as compared to PO and PI the angles α, β and δ are also small then,
   α ≈ α = `"PA"/"PO"; and beta ≈ tan beta = "PA"/"PI"`
   Then, `δ = "PA"/"PO" + "PA"/"PI"`
   Here, PA = h, PO = - u and PI = v
   `δ = "h"/(-"u") + "h"/"v" = "h"(1/(- "u") + 1/"v")`
   After rearranging, 
   `δ = "h"(1/"v" - 1/"u") = "h"/"f"`
   `δ = "h"/"f"`
4. For a parallel ray that falls on the arrangement, the two lenses produce deviations δ₁ and δ₂ respectively and The net deviation δ is
   

   δ = δ₁ + δ₂

   δ₁ = `"h"_1/"f"_1`
   δ₂ = `"h"_2/"f"_2`
   δ = `"h"_1/"f"`   .....(1)
   `"h"_1/"f" = "h"_1/"f"_1 + "h"_2/"f"_2`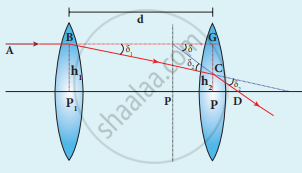
   
   Lens in out of contact
   From the geometry,
   h₂ – h₁ = P₂G – P₁G = CG
   h₂ – h₁ = BG tan δ₁ ≈ BG δ₁
   h₂ – h₁ = `("dh"_1)/"f"_1`
   h₂ = h₁ + `("dh"_1)/"f"_1`    .....(2)
   `"h"_1/"f" = "h"_1/"f"_1 + "h"_2/"f"_2 + ("h"_1"d")/("f"_1"f"_2)`
   On further simplification,
   `1/"f" = 1/"f"_1 + 1/"f"_2 + "d"/("f"_1"f"_2)`
   The above equation could be used to find the equivalent focal length.
   To find the position of the equivalent lens, we can further write from the geometry.
   PP₂ = EG = `"GC"/(tan δ)`
   PP₂ = EG = `("h"_1 - "h"_2)/(tan δ) = ("h"_1 - "h"_2)/δ`
   

   From equation (1) and (2)
   h₂ – h₁ = d`"h"_1/"f"_1` and
   δ = `"h"_1/"f"`
   PP₂ = `["d" "f"/"f"_1]`
   The position of the equivalent single lens from the second lens. Its position from the first lens.
   PP₁ = d – `["d" "f"/"f"_1]`;
   PP₁ = d`[1 – "f"/"f"_1]`