Question

Describe the microscopic model of current and obtain general form of Ohm’s law.

Answer 1

1. XY is a conductor of an area of cross-section A
2. E is the applied electric field.
3. n is the number of electrons per unit volume with the same drift velocity (v_d)

Let electrons move through a distance dx in time interval dt.

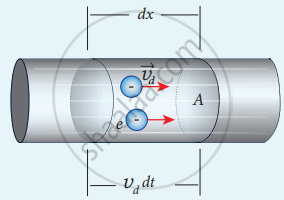
Microscopic model of the current

`therefore "vd" = "dx"/"dt"`

dx = v_d . dt …………(1)

Electrons available in the given volume
= volume × number per unit volume
= A. dx × n
= A . v_d dt × n [From (1)]

Total charge in volume dQ = charge × number of electrons
dQ = (e) (Av_d dt) n

w.k.t, I = `"dQ"/"dt"`

∴ I = `("neAv"_"d""dt")/"dt"`

I = nAev_d   .....(2)

Current density, J = `1/"A"`

∴ J = `("neAv"_"d")/"A"`

J = nev_d

In vector form, `vec"J" = "ne" vec"V"_"d"`

Substitutingthe value of `vec"V"_"d" = ("e"tau)/"m"*vec"E"`    .....(2)

`vec"J" = ("ne"^2tau)/"m"`

This is the microscopic form of Ohm's law

J = `sigma vec"E"`

`sigma = ("ne"^2tau)/"m"`