Question

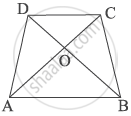
Diagonals AC and BD of a trapezium ABCD intersect at O, where AB || DC. If `(DO)/(OB) = 1/2,` then show that AB = 2CD

Answer 1

Given: 

1. In trapezium ABCD
   Diagonals AC and BD intersect at O
2. AB || DC
3. `(DO)/(OB) = 1/2`

To prove: 

AB = 2CD

Proof:

In ΔOAB and ΔOCD

∠AOB = ∠COD       ...(vertically opposite angle)

∠OAB = ∠OCD        ....(Alternate interior angle as given, AB || DC)

ΔOAB ∼ ΔOCD      ...(by AA similarity Rule)

Now, `(OC)/(OA) = (CD)/(AB) = (DO)/(BO)`

⇒ `(CD)/(AB) = (DO)/(BO)`

`(CD)/(AB) = 1/2`      ....(given)

Hence, AB = 2CD   Proved