Question

Discuss about simple microscope and obtain the equations for magnification for near point focusing and normal focusing.

Answer 1

• A simple microscope is a single magnifying (converging) lens of small focal length.
• The idea is to get an erect, magnified and virtual image of the object. For this the object is placed between F and P on one side of the lens and viewed from other side of the lens.

1. Near point focusing:
   The image is formed at a near point, i.e. 25 cm for the normal eye. This distance is also called as least distance D of distinct vision. In this position, the eye feels comfortable but there is little strain on the eye.
2. Normal focusing:
   The image is formed at infinity. In this position, the eye is most relaxed to view the image.

Magnification in near point focusing:

1. Object distance u is less than f. The image distance is the near point D. The magnification m is given by the relation,
   m = `"v"/"u"`
2. The magnification can further be written as,
   m = `1 - "v"/"f"`(using lens equation)
   Substituting for ν with sign convention,
   v = - D
   m = `1 + "D"/"f"`
   This is the magnification for near-point focusing.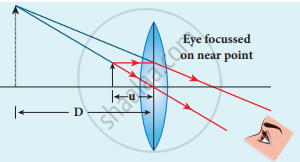
   
   Near point focusing

Magnification in normal focusing (angular magnification):

1. The magnification for the image is formed at infinity.
2. The angular magnification is defined as the ratio angle θ_i, subtended by the image with an aided eye to the angle θ₀ subtended by the object with unaided eye.
   m = `theta_"i"/theta_0`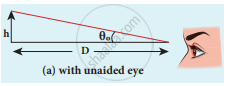
   
   
   
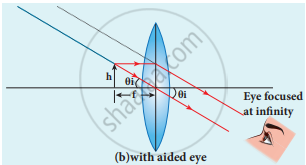
   Normal focusing

For unaided eye

tan θ₀ ≈ θ₀ = `"h"/"D"`

For aided eye

tan θ₀ ≈ θ₀ = `"h"/"f"`

The angular magnification is,

m = `theta_"i"/theta_0 = ("h"//"f")/("h"//"D")`

m = `"D"/"f"`

This is the magnification for normal focusing.