Advertisements
Advertisements
Question
Draw a line segment AB = 7 cm and mark a point P on it. Draw a line perpendicular to the given line segment at P
Solution
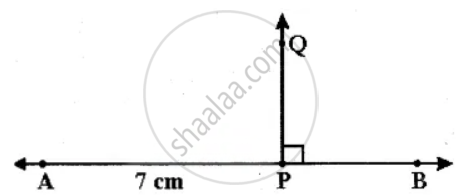
Step 1: Draw a line AB = 7 cm and take a point P anywhere on the line.
Step 2: Place the set square on the line in such a way that the vertex which forms right angle coincides with P and one arm of the right angle coincides with the line AB.
Step 3: Draw a line PQ through P along the other arm of the right angle of the set square.
Step 4: The line PQ is perpendicular to the line AB at P.
That is, PQ ⊥ AB
∠APQ = ∠BPQ = 90°
APPEARS IN
RELATED QUESTIONS
Draw line l. Take any point P on the line. Using a set square, draw a line perpendicular to line l at the point P.
Draw a line AB. Using a compass, draw a line perpendicular to AB at the point B.
Draw line CD. Take any point M on the line. Using a protractor, draw a line perpendicular to line CD at the point M.
Take a point R on line XY. Draw a line perpendicular to XY at R, using a set square.
Number of set squares in the geometry box is ______.
The common properties in the two set-squares of a geometry box are that they have a ______ angle and they are of the shape of a ______.
Two perpendiculars can be drawn to a given line from a point not lying on it.
Using only the two set-squares of the geometry box, an angle of 40° can be drawn.
Using only the two set-squares of the geometry box, an angle of 15° can be drawn.
Draw a line l and point X on it. Through X, draw a line segment `overline"XY"` perpendicular to l.
Now draw a perpendicular `overline"XY"` to at Y. (use ruler and compasses)
