Question

Draw Average Variable Cost, Average Total Cost ad Marginal Cost curves in a single diagram.

Answer 1

Average Variable Cost (AVC), Average Total Cost (ATC) and Marginal Cost (MC) curves:

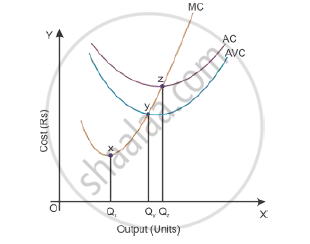
Relationship between ATC (or AC) and MC
1. When ATC is falling, MC falls at a faster rate; and MC remains below ATC curve.
2. When AC is rising, MC rises at a faster rate; and MC remains above ATC curve.
3. When AC is at its minimum point, (z), MC is equal to ATC.
4. MC curve cuts ATC curve at its minimum point.
5. ATC and MC are both U-shaped curve reflecting the Law of Variable Proportions.
6. While ATC includes both variable as well as fixed cost, whereas, MC includes only the variable cost.
7. ATC (or AC) and MC are both derived from TC as:
\[i . e . AC = \frac{TC}{Q}\]
\[\text{ and MC }= \frac{∆ TC}{∆ Q}\]