Question

Draw a circle of radius 3 cm. Draw a pair of tangents to this circle, which are inclined to each other at an angle of 60º.

Answer 1

Steps of construction

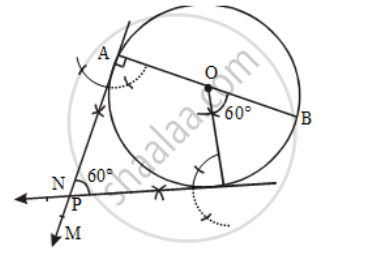
Step I: Draw a circle with O as centre and radius = 3 cm.

Step II: Draw any diameter AOB of this circle.

Step III: Construct ∠BOC = 60º such that radius OC meets the circle at C.

Step IV: Draw AM ⊥ AB and CN ⊥OC.

Let AM and CN intersect each other at P.

Then, PA and PC are the desired tangents to the given circle, inclined at an angle of 60º

Proof: ∠AOC = (180º – 60º) = 120º

In quad. OAPC, we have

∠OAP = 90º, ∠AOC = 120º, ∠OCP = 90º.

∴∠APC = [360º – (90º + 120º + 90º)] = 60º