Advertisements
Advertisements
Question
Draw the line(s) of symmetry for the figure drawn below:
Solution
APPEARS IN
RELATED QUESTIONS
Complete the following table:
| Point | Reflection in | ||
| x-axis | y-axis | origin | |
| (i) (8, 2) | |||
| (ii) (5, 6) | |||
| (iii) (4, −5) | |||
| (iv) (6, −2) | |||
| (v) (−3, 7) | |||
| (vi) (−4, 5) | |||
| (vii) (−2, −7) | |||
| (viii) (−6, −3) | |||
| (ix) (4, 0) | |||
| (x) (−7, 0) | |||
| (xi) (0, −6) | |||
| (xii) (0, 7) | |||
| (xiii) (0, 0) | |||
A point P (7,3) is reflected in the x-axis to point P’. The point P’ is further reflected in v-axis to point P” Find :
(i) the coordinates of P’
(ii) the co-ordinates of P”
(iii) the image of P (7, 3) in origin.
The point P (3, – 8) is reflected in origin to point Q. The Point Q is further reflected in the x-axis to point R. Find :
(i) the co-ordinates of Q
(ii) the co-ordinates of R
(iii) the image of P (3, – 8) in the y-axis.
Mark points A (4, 5) and B (− 5, 4) on a graph paper. Find A’, the image of A in x-axis and B’, the image of B in x-axis.
Mark A’ and B’ also on the same graph paper. Join AB and A’ B’ and find if AB = A’ B’?
Mark points A (– 6, 5) and B (– 4, – 6) on a graph paper. Find A’, the image of A in origin and B’, the image of B in origin. Mark A’ and B’ also on the same graph paper. Join AB and A’ B’. Is AB = A’ B’?
The three digit number 101 has rotational and reflection symmetry. Give five more examples of three digit numbers which have both rotational and reflection symmetry
Draw the following:
A figure which has both reflection and rotational symmetry
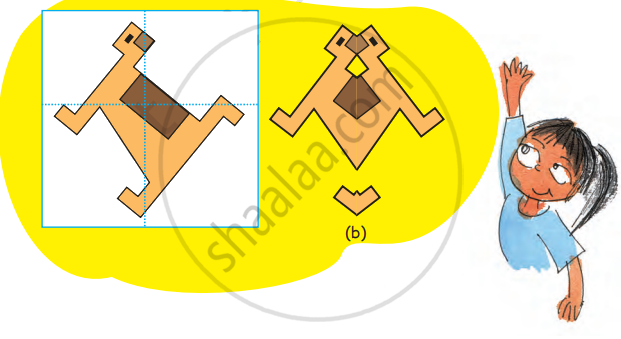
Look at the figure in the white box. On which of the dotted lines will you keep the mirror so that you get shape (b)? Also, tell which part of the picture will be hidden when we keep the mirror on the dotted line.
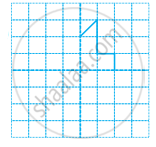
Copy the following drawing on squared paper. Complete such that the resulting figure has two dotted lines as two lines of symmetry.
How did you go about completing the picture?
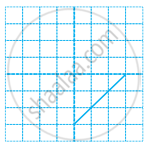
Copy the following drawing on squared paper. Complete such that the resulting figure has two dotted lines as two lines of symmetry.
How did you go about completing the picture?