Advertisements
Advertisements
Question
Draw what the following shapes would look like on a `1/4` turn and half a turn.
| On `1/4` turn | On half turn | |
a)  |
||
b)  |
||
c)  |
||
d)  |
- Which of the above shapes do not look the same on the `1/4` turn?
- Which shapes do not look the same on `1/2` a turn?
Solution
| On `1/4` turn | On half turn | |
a)  |
||
b)  |
||
c)  |
||
d)  |
 |
 |
- Image (a), (c), and (d) do not look the same on the `1/4` turn.
- Image (a) does not look the same on the `1/2` turn.
APPEARS IN
RELATED QUESTIONS
Given the line(s) of symmetry, find the other hole(s):
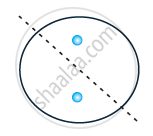
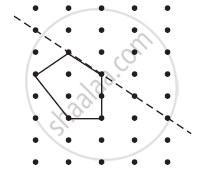
In the given figure, the mirror line (i.e., the line of symmetry) is given as a dotted line. Complete given figure performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure you complete?

The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry.
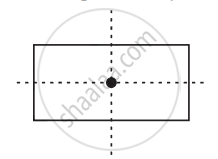 |
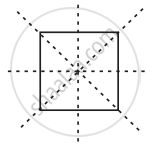 |
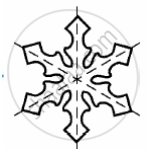 |
| (a) | (b) | (c) |
Identify multiple lines of symmetry, if any, in the following figure.

Copy the figure given here.

Take any one diagonal as a line of symmetry and shade a few more squares to make the figure symmetric about a diagonal. Is there more than one way to do that? Will the figure be symmetric about both the diagonals?
Copy the diagram and complete the given shape to be symmetric about the mirror line(s):
State the number of lines of symmetry for a rectangle figure.
What letters of the English alphabet have reflectional symmetry (i.e., symmetry related to mirror reflection) about both horizontal and vertical mirrors.
Draw the line of symmetry in the following figure.
How many lines of symmetry for the following figure
Which of the following letters of English alphabets have more than 2 lines of symmetry?
