Advertisements
Advertisements
Question
एक गोल मेजपोश पर छ: समान डिजाइन बने हुए हैं जैसा की दी गई आकृति में दर्शाया गया है। यदि मेजपोश की त्रिज्या 28 सेमी है, तो 0.35 रु प्रति वर्ग सेंटीमीटर की दर से इन डिजाइनों को बनाने की लागत ज्ञात कीजिए।
[`sqrt3 = 1.7` का प्रयोग करें]
Solution
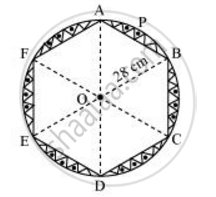
यह देखा जा सकता है कि ये डिज़ाइन वृत्त के खंड हैं।
खंड APB पर विचार करें। जीवा AB षट्भुज की एक भुजा है। प्रत्येक जीवा वृत्त के केंद्र में `(360º)/6` = 60º को प्रतिस्थापित करेगी।
ΔOAB में,
∠OAB = ∠OBA (As OA = OB)
∠AOB = 60°
∠OAB + ∠OBA + ∠AOB = 180°
2∠OAB = 180° − 60° = 120°
∠OAB = 60°
अतः ΔOAB एक समबाहु त्रिभुज है।
ΔOAB का क्षेत्रफल = `sqrt3/4 xx ("side")^2`
`=sqrt3/4 xx (28)^2 `
` = 196sqrt3`
` = 196 xx 1.7 `
= 333.2 cm2
क्षेत्र OAPB का क्षेत्रफल = `60^@/360^@ xx pir^2`
`= 1/6xx 22/7xx28xx28`
`= 1232/3 cm^2`
खंड ΔAPB का क्षेत्रफल = त्रिज्यखंड OAPB का क्षेत्रफल - ΔOAB का क्षेत्रफल
`=(1232/3 - 333.2) cm^2`
= `6xx(1232/3 - 333.2) cm^2`
`= (2464 - 1999.2)cm^2`
= 464.8 cm2
1 cm2 डिज़ाइन बनाने की लागत = 0.35 रुपये
464.76 cm2 डिजाइन बनाने की लागत = 464.8 × 0.35 = रु 162.68
इसलिए इस तरह के डिजाइन बनाने की लागत 162.68 रुपये है।
APPEARS IN
RELATED QUESTIONS
दो वृत्तों की त्रिज्याएँ क्रमश: 8 सेमी और 6 सेमी हैं। उस वृत्त की त्रिज्या ज्ञात कीजिए जिसका क्षेत्रफल इन दोनों वृत्तों के क्षेत्रफलों के बराबर है।
निम्नलिखित में से सही उत्तर पर निशान लगाएँ और अपनी पसंद का औचित्य सिद्ध करें: यदि एक वृत्त का परिमाप और क्षेत्रफल संख्यात्मक रूप से बराबर है, तो उस वृत्त की त्रिज्या है:
त्रिज्या R वाले वृत्त के उस त्रिज्यखंड का क्षेत्रफल जिसका कोण p° है, निम्नलिखित है ______.
दी गई आकृति एक दौड़ने का पथ दर्शाती है, जिसके बाएँ और दाएँ सिरे अर्धवृत्ताकार हैं।
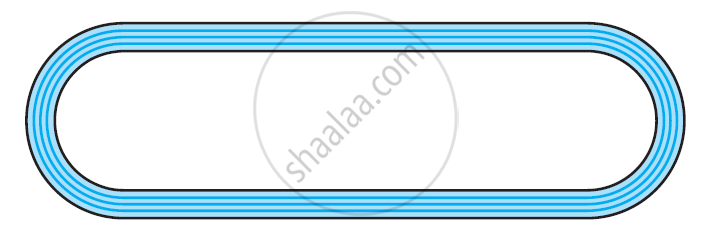
दोनों आंतरिक समांतर रेखाखंडों के बीच की दूरी 60 मी है तथा इनमें से प्रत्येक रेखाखंड 106 मी लंबा है। यदि यह पथ 10 मी चौड़ा है, तो ज्ञात कीजिए।
- पथ के आंतरिक किनारों के अनुदिश एक पूरा चक्कर लगाने में चली गई दूरी
- पथ का क्षेत्रफल
[उपयोग Π = 22/7]
यदि एक वृत्त की परिधि और एक वर्ग का परिमाप बराबर है, तो ______।
त्रिज्या के एक अर्धवृत्त के अंतर्गत खींचे जा सकने वाले सबसे बड़े त्रिभुज का क्षेत्रफल ______ है।
किसी स्थान पर 16 m और 12 m व्यास वाले दो वृत्ताकार पाकों के क्षेत्रफलों के योग के बराबर क्षेत्रफल का एक अकेला वृत्ताकार पार्क बनाने का प्रस्ताव है। नये पार्क की त्रिज्या होगी ______ ।
क्या यह कहना सत्य होगा कि त्रिज्या a cm वाले एक वृत्त के परिगत वर्ग का परिमाप 8 cm है? अपने उत्तर का कारण दीजिए।
क्या यह कहना सत्य है कि व्यास p cm वाले एक वृत्त के अंतर्गत वर्ग का क्षेत्रफल p2 cm2 है? क्यों?
आकृति में, छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए, जहाँ A, B, C और D को केंद्र मान कर खींचे गये चाप युगम में वर्ग ABCD की क्रमशः AB, BC, CD और DA भुजाओं के मध्य-बिद्ओं P, Q, R और S पर प्रतिच्छेद करते हैं (π = 3.14 का प्रयोग कीजिए)।

