Advertisements
Advertisements
Question
एक खेत समलंब के आकार का है जिसकी समांतर भुजाएँ 25 मी और 10 मी हैं। इसकी असमांतर भुजाएँ 14 मी और 13 मी हैं। इस खेत का क्षेत्रफल ज्ञात कीजिए।
Solution
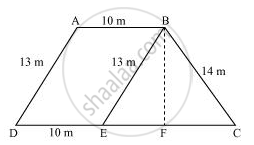
AD के समांतर एक रेखा BE खींचिए और CD पर एक लंब BF खींचिए।
यह देखा जा सकता है कि ABED एक समांतर चतुर्भुज है।
BE = AD = 13 m
ED = AB = 10 m
EC = 25 − ED = 15 m
ΔBEC के लिये,
अर्ध-परिधि,
`s=(13+14+15)/2=21 m`
हीरोन के सूत्र से,
`"त्रिभुज का क्षेत्रफल" = sqrt(s(s-a)(s-b)(s-c))`
`"क्षेत्र ΔBEC "=[sqrt(21(21-13)(21-14)(21-15))]m^2`
`=[sqrt(21(8)(7)(6))]m^2`
= 84 m2
`"क्षेत्र ΔBEC "=1/2xxCExxBF`
`rArr84=1/2xx15xxBF`
`rArrBF=168/15=11.2 m`
क्षेत्र ABED = BF × DE = 11.2 × 10 = 112 m2
मैदान का क्षेत्रफल = 84 + 112 = 196 m2
APPEARS IN
RELATED QUESTIONS
राधा ने एक रंगीन कागज़ से एक हवाईजहाज़ का चित्र बनाया, जैसा कि आकृति में दिखाया गया है। प्रयोग किए गए कागज़ का कुल क्षेत्रफल ज्ञात कीजिए।
एक समचतर्भजाकार घास के खेत में 18 गायों के चरने के लिए घास है। यदि इस समचतुर्भुज की प्रत्येक भुजा 30 मी है और बड़ा विकर्ण 48 मी है, तो प्रत्येक गाय को चरने के लिए इस घास के खेत का कितना क्षेत्रफल प्राप्त होगा?
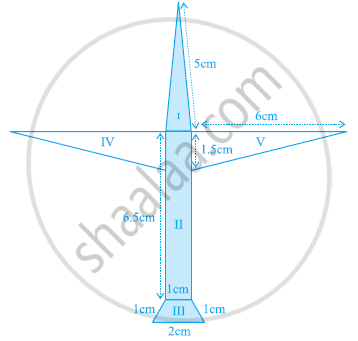
एक पतंग तीन भिन्न-भिन्न रंगों के कागज़ों से बनी है। इन्हें आकृति में I, II और III से दर्शाया गया है। पतंग का ऊपरी भाग 32 सेमी विकर्ण का एक वर्ग है और निचला भाग 6 सेमी, 6 सेमी और 8 सेमी भुजाओं का एक समद्विबाहु त्रिभुज है। ज्ञात कीजिए कि प्रत्येक रंग का कितना कागज़ प्रयुक्त किया गया है।
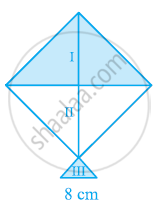
एक समद्विबाहु त्रिभुज का क्षेत्रफल `5/4 sqrt(11)` cm2 होगा, यदि उसका परिमाप 11 cm है और आधार 5 cm है।
एक फ्लाईओवर की त्रिभुजाकार पार्श्व दीवारों को विज्ञापनों के लिए प्रयोग किया जाता है। दीवारों की भुजाएँ 13 m, 14 m और 15m हैं। विज्ञापनों से एक वर्ष में 2000 रु प्रति m2 की दर से आय होती है। एक कंपनी इनमें से एक दीवार को 6 महीने के लिए किराए पर लेती है। उस कंपनी ने कितना किराया दिया होगा?
एक खेत एक समांतर चतुर्भुज के आकार का है, जिसकी भुजाएँ 60 m और 40 m हैं तथा एक विकर्ण 80 m है। इस खेत का क्षेत्रफल ज्ञात कीजिए।
एक चतुर्भुज ABCD की भुजाएँ (एक क्रम में लेने पर) 6 cm, 8 cm, 12 cm और 14 cm हैं तथा प्रथम दो भुजाओं के बीच का कोण समकोण है। इसका क्षेत्रफल ज्ञात कीजिए।
एक मकान का निर्माण करने के लिए एक आयताकार भूखंड दिया गया, जिसकी लंबाई 40 m है तथा सामने की चौडाई 15 m है। नियमों के अनुसार, सामने और पीछे की ओर न्यूनतम 3 m चौड़ी जगह तथा प्रत्येक अन्य ओर पर न्यूनतम 2 m चौड़ी जगह छोड़नी आवश्यक है। वह अधिकतम क्षेत्र ज्ञात कीजिए जिसमें मकान का निर्माण किया जा सकता है।
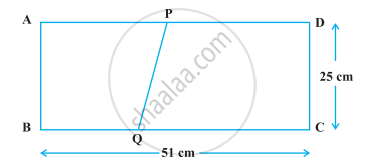
एक आयत ABCD की विमाएँ 51 cm × 25 cm हैं। इस आयत में से एक समलंब PQCD काटा जाता है, जिसकी समांतर भुजाएँ QC और PD हैं और ये 9 : 8 के अनुपात में हैं, जैसा कि निम्नलिखित आकृति में दर्शाया गया है। यदि समलंब PQCD का क्षेत्रफल आयत के क्षेत्रफल का `5/6` भाग है, तो QC और PD की लंबाइयाँ ज्ञात कीजिए।
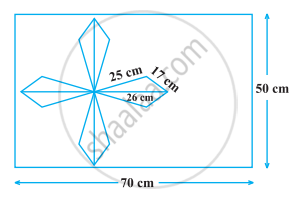
50 cm × 70 cm विमाओं वाली एक आयताकार टाइल पर, निम्नलिखित आकृति में दर्शाए अनुसार एक डिज़ाइन बनाया जाता है। इस डिज़ाइन में 8 त्रिभुज हैं, जिनमें से प्रत्येक की भुजा 26 cm, 17 cm और 25 cm की हैं। डिज़ाइन का पूर्ण क्षेत्रफल ज्ञात कीजिए तथा टाइल के शेष भाग का क्षेत्रफल भी ज्ञात कीजिए।