Question

एका समभुज चौकोनाचा एक कर्ण 30 सेमी असून त्याचे क्षेत्रफळ 240 चौसेमी आहे. तर त्या चौकोनाची परिमिती काढा.

Answer 1

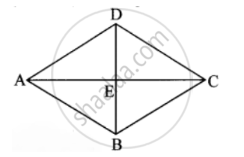
ABCD हा समभुज चौकोन समजा.

कर्ण AC आणि BD हे बिंदू E वर छेदतात.

l(AC) = 30 सेमी     ...(i)

आणि समभुज चौकोनाचे क्षेत्रफळ = 240 चौ.सेमी         ...(ii)

समभुज चौकोनाचे क्षेत्रफळ = `1/2` (निदानांचा गुणाकार)

⇒ 240 = `1/2` × (30 × DB)

⇒ DB = `(240 xx 2)/30`

⇒ DB = 16           ...(iii)

समभुज चौकोनाचे कर्ण एकमेकांना दुभाजक करतात.

∴ `l(AE) = 1/2 l(AC)`

= `1/2 xx 30`

= 15 सेमी           ...(iv)

∴ `l(DE) = 1/2 l(DB)`

= `1/2 xx 16`

= 8 सेमी           ...(v)

ΔADE मध्ये,

∠AED = 90°               …[समभुज चौकोनाचे कर्ण एकमेकांना लंब असतात.]

AE² + DE² = AD²              …[पायथागोरस प्रमेय]

⇒ 15² + 8² = AD²              ...[(iv) आणि (v) वरून]

⇒ AD² = 225 + 64

⇒ AD² = 289

⇒ AD = `sqrt289`             …[दोन्ही बाजूंचे वर्गमूळ घेऊन]

= 17 सेमी

अशा प्रकारे, समभुज चौकोनाची बाजू = 17 सेमी

समभुज चौकोनाची परिमिती = 4 × बाजू 

= `4 xx 17`

= 68 सेमी

∴ समभुज चौकोनाची परिमिती 68 सेमी आहे.