Question

Equal current i flows in two segments of a circular loop in the direction shown in figure. Radius of the loop is r. The magnitude of magnetic field induction at the centre of the loop is ______.

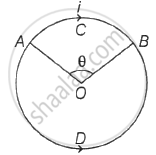
Options

• zero

• `(mu_0"i"theta)/(3pi"r")`

• `mu_0/(2pi)"i"/"r"(pi-theta)`

• `mu_0/(2pi)."i"/"r"(2pi-theta)`

Answer 1

Equal current i flows in two segments of a circular loop in the direction shown in figure. Radius of the loop is r. The magnitude of magnetic field induction at the centre of the loop is `underlinebb(mu_0/(2pi)"i"/"r"(pi-theta))`.

Explanation:

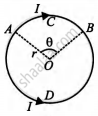
Magnetic field induction at O due to current through ACB is

B₁ = `mu_0/(4pi)("I"theta)/"r"`

It is acting perpendicular to the paper downwards.

Magnetic field induction at O due to current through ADB is

B₂ = `mu_0/(4pi)"I"/"r"(2pi-theta)`

It is acting perpendicular to paper upwards.

∴ Total magnetic field at O due to current loop is

B = B₂ - B₁ =  `mu_0/(4pi)"I"/"r"(2pi-theta)- mu_0/(4pi)"I"/"r"theta= mu_0/(2pi)"I"/"r"(pi-theta)`

acting perpendicular to paper upwards.