Advertisements
Advertisements
Question
Explain how overtone is produced in a closed organ pipe.
Solution
If one end of a pipe is closed, the wave reflected at this closed-end is 180° out of phase with the incoming wave. So, there is no displacement of the particles at the closed end. Hence, nodes are formed at the closed end and anti-nodes are formed at the open end.
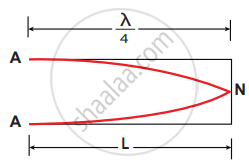
No motion of particles which leads to nodes at closed-end and antinodes at the open end (fundamental mode) (N-node, A-antinode)
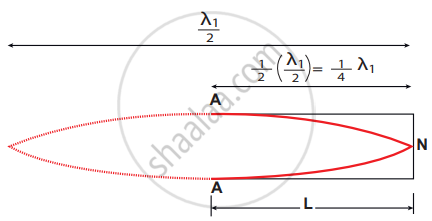
Consider the simplest mode of vibration of the air column called the fundamental mode. Anti-node is formed at the open end and node at the closed end. From the above figure, let L be the length of the tube and the wavelength of the wave produced. For the fundamental mode of vibration, we have,
– L = `lambda_1/4` (or)
Wave length λ1 = 4L
The frequency of the note emitted is
`"f"_1 = "v"/lambda_1 = "v"/(4"L")`
which is called the fundamental note.
The frequencies higher than the fundamental frequency can be produced by blowing air strongly at the open end. Such frequencies are called overtones.
The second mode of vibration in open pipes is shown in the figure.
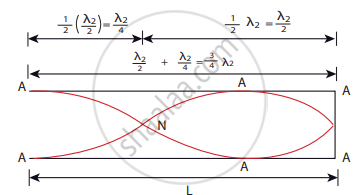
Second mode of vibration having two nodes and two anti-nodes
4L = 3λ2
L = `(3lambda_2)/4` (or) `lambda_2 = (4"L")/3`
The frequency for this,
`"f"_2 = "v"/lambda_2 = (3"v")/(4"L") = 3 "f"_1`
is called the first overtone, since here, the frequency is three times the fundamental frequency it is called third harmonic. The Figure shows the third mode of vibration having three nodes and three anti-nodes.

Third mode of vibration having three nodes and three anti-nodes
We have, 4L = 5λ3
L = `(5lambda_3)/4` (or) `lambda_3 = (4"L")/5`
The frequency,
`"f"_3 = "v"/lambda_3 = "5v"/"4L" = 5"f"_1`
is called the second overtone, and since n = 5 here, this is called fifth harmonic. Hence, the closed organ pipe has only odd harmonics and the frequency of the nth harmonic is fn = (2n+l)f1. Hence, the frequencies of harmonics are in the ratio,
f1 : f2 : f3 : f4 = 1 : 3 : 5 : 7 : …
APPEARS IN
RELATED QUESTIONS
Which of the following options is correct?
| A | B |
| (1) Quality | (A) Intensity |
| (2) Pitch | (B) Waveform |
| (3) Loudness | (C) Frequency |
Options for (1), (2) and (3), respectively are
A man sitting on a swing which is moving to an angle of 60° from the vertical is blowing a whistle which has a frequency of 2.0 k Hz. The whistle is 2.0 m from the fixed support point of the swing. A sound detector which detects the whistle sound is kept in front of the swing. The maximum frequency the sound detector detected is
Define intensity of sound.
Define loudness of sound.
Write a short note on intensity.
Write a short note on loudness.
Explain how overtone is produced in a Open organ pipe.
Let the source propagate a sound wave whose intensity at a point (initially) be I. Suppose we consider a case when the amplitude of the sound wave is doubled and the frequency is reduced to one-fourth. Calculate now the new intensity of sound at the same point?
Why is the roar of our national animal different from the sound of a mosquito?
In an empty room why is it that a tone sounds louder than in the room having things like furniture etc.
