Advertisements
Advertisements
Question
Explain the principle of potentiometer.
Solution
Principle:
The potential difference between any two points of the potentiometer wire is directly proportional to the length of wire between these two points.
The fall of potential per unit length of potentiometer wire (potential gradient of wire) is
constant.
Explanation:
a) Suppose a potentiometer wire AB of length L and resistance R is stretched on the
rectangular wooden board. The source of e.m.f E and negligible internal resistance is
connected to the wire AB through a key K as shown in figure.
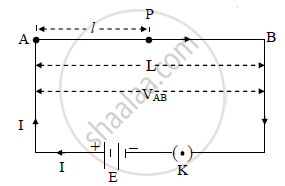
b) Resistance per unit length of wire AB is given by, σ = R/L
∴ R = σL
c) Let ‘VAB’ be the P.D across the wire. There is uniform fall of potential along the wire
from A to B.
d) By Ohm’s law, the current ‘I’ passing through the wire is given by,

e) Let ‘P’ be any point on the wire, such that AP = ‘l’. The resistance of wire AP of
length ‘l’ is RAP = σl. So the potential difference ‘V’AP between points A and P is given
by,
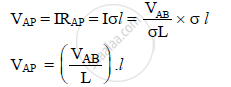
f) But, VAB and L are constant,
∴ VAP ∝ L
∴ `V_(AP)/L` = K = constant
where, K is called potential gradient of wire.
APPEARS IN
RELATED QUESTIONS
Two diametrically opposite points of a metal ring are connected to two terminals of the left gap of meter bridge. The resistance of 11 Ω is connected in right gap. If null point is obtained at a distance of 45 cm from the left end, find the resistance of metal ring.
An unknown resistance is placed in the left gap and resistance of 50 ohm is placed in the right gap of a meter bridge. The null point is obtained at 40 cm from the left end. Determine the unknown resistance.
When unknown resistance is determined by meter bridge, the error due to contact resistance
is minimized ______.
(A) by connecting both the resistances only in one gap.
(B) by interchanging the positions of known and unknown resistance.
(C) by using uniform wire.
(D) by obtaining the null point near the ends of the wire.
A potentiometer wire has length of 2m and resistance 10Ω. It is connected in series with resistance 990Ω and a cell of e.m.f. 2V. Calculate the potential gradient along the wire.
