Advertisements
Advertisements
Question
Explain the variation of g with latitude.
Solution
When an object is on the surface of the Earth, it experiences a centrifugal force that depends on the latitude of the object on Earth. If the Earth were not spinning, the force on the object would have been mg. However, the object experiences an additional centrifugal force due to the spinning of the Earth.
This centrifugal force is given by mω2R’.
OPz, cos λ = `"PZ"/"OP" = "R’"/"R"`
R’ = R cos λ

Variation of g with latitude
where λ is the latitude. The component of centrifugal acceleration experienced by the object in the direction opposite to g is
aPQ = ω2R’ cos λ = ω2R cos2 λ
Since R’ = R cos λ
Therefore, g’ = g – ω2 R cos2 λ
From the above expression, we can infer that at the equator, λ = 0, g’ = g – ω2R. The acceleration due to gravity is minimum. At poles λ = 90; g’ = g, it is maximum. At the equator, g’ is minimum.
APPEARS IN
RELATED QUESTIONS
Is there any meaning of "Weight of the earth"?
If heavier bodies are attracted more strongly by the earth, why don't they fall faster than the lighter bodies?
If the acceleration due to gravity at the surface of the earth is g, the work done in slowly lifting a body of mass m from the earth's surface to a height R equal to the radius of the earth is
Find the acceleration due to gravity in a mine of depth 640 m if the value at the surface is 9.800 m s−2. The radius of the earth is 6400 km.
Explain the variation of g with altitude.
Calculate the change in g value in your district of Tamil nadu. (Hint: Get the latitude of your district of Tamil nadu from Google). What is the difference in g values at Chennai and Kanyakumari?
The earth is an approximate sphere. If the interior contained matter which is not of the same density everywhere, then on the surface of the earth, the acceleration due to gravity ______.
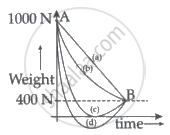
A person whose mass is 100 kg travels from Earth to Mars in a spaceship. Neglect all other objects in the sky and take acceleration due to gravity on the surface of the Earth and Mars as 10 m/s2 and 4 m/s2 respectively. Identify from the below figures, the curve that fits best for the weight of the passenger as a function of time.
If R is the radius of the earth and g is the acceleration due to gravity on the earth's surface, the mean density of the earth is ______.
The percentage decrease in the weight of a rocket, when taken to a height of 32 km above the surface of the earth will, be ______.
(Radius of earth = 6400 km)
