Advertisements
Advertisements
Question
Explain why a cyclist bends while negotiating a curve road? Arrive at the expression for angle of bending for a given velocity.
Solution
Let us consider a cyclist negotiating a circular level road (not banked) of radius r with a speed v. The cycle and the cyclist are considered as one system with mass m. The center gravity of the system is C and it goes in a circle of radius r with center at O. Let us choose the line OC as X-axis and the vertical line through O as Z-axis as shown in Figure.
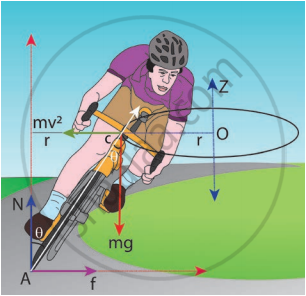
Bending of cyclist
The system as a frame is rotating about Z-axis. The system is at rest in this rotating frame. To solve problems in a rotating frame of reference, we have to apply a centrifugal force (pseudo force) on the system which will be `(mv^2)/r` This force will act through the center of gravity. The forces acting on the system are,
- gravitational force (mg)
- normal force (N)
- frictional force (f)
- centrifugal force `((mv^2)/r)`.
As the system is in equilibrium in the rotational frame of reference, the net external force and net external torque must be zero. Let us consider all torques about point A in Figure.
For rotational equilibrium,
τnet = 0
The torque due to the gravitational force about point A is (mg AB) which causes a clockwise turn that is taken as negative. The torque due to the centripetal force is I BC which causes an (`(mv^2)/r` BC) Which causes an anticlockwise turn that is taken as positive.
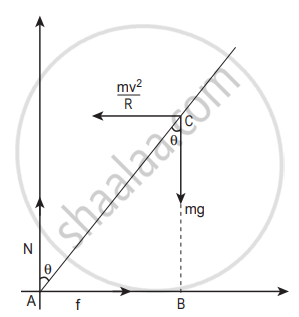
Force diagram for the cyclist in turns
`-mg AB + (mv^2)/r BC = 0`
mg AB = `(mv^2)/r`BC
From ΔABC
AB = AC sin θ and BC = AC cos θ
mg AC sin θ = `(mv^2)/r` AC cos θ
tan θ = `v^2/(rg)`
θ = `tan^-1(v^2/(rg))`
While negotiating a circular level road of radius r at velocity v, a cyclist has to bend by an angle 0 from vertical given by the above expression to stay in equilibrium (i.e. to avoid a fall).
APPEARS IN
RELATED QUESTIONS
A couple produces, ______
What is equilibrium?
How do you distinguish between stable and unstable equilibrium?
Define couple.
State principle of moments.
Define centre of gravity.
Explain the types of equilibrium with suitable examples.
Explain the method to find the center of gravity of an irregularly shaped lamina.
