Question

Figure show the circular coil carrying current I kept very close but not touching at a point A on a straight conductor carrying the same current l. The magnitude of magnetic induction at the centre of the circular coil will be.

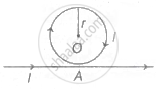
Options

• `(mu_0l)/(2"r") (1 + 1/pi)`

• `(mu_0l)/(2pi"r")`

• `(mu_0l)/(2"r")`

• None of above

Answer 1

None of above

Explanation:

Magnetic induction at the centre of circular current-carrying loop,

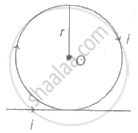
`"B"_1 = (mu_0"i")/"2r"`    (downward direction)

Magnetic induction at the centre 0 due to straight wire,

`"B"_2 = (mu_0)/(2pi) * "i"/"r"`  (upward direction)

Net magnetic induction at O,

B = B₁ - B₂ = `(mu_0"i")/"2r" - mu_0/(2pi) * "i"/"r"`

`= (mu_0"i")/"2r" [1 - 1/pi]`   [downward direction]

Hence, there are no option correct.