Advertisements
Advertisements
Question
Find, by integration, the volume of the container which is in the shape of a right circular conical frustum as shown in the Fig 9.46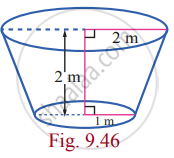
Solution
By using integration we have to find the volume of the frustum.
So first find the equation of the curve.
Let A(0, 1) and B(2, 2) be two points.
Line joining these two points form a straight line.
That straight line revolves around x-axis.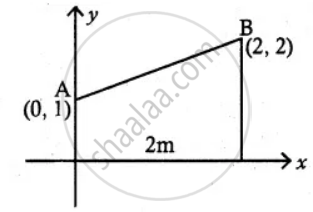
Equation AB is `(y - 1)/(2 - 1) = (x 0)/(2 - 0)`
`(y - 1)/1 = x/2`
`y - 1 = x/2`
y = `x/2 + 1`
y = `(x + 2)/2`
Volume of the solid revolves around x-axis
= `pi int_"a"^"b" y^2 "d"x`
= `pi int_0^2 (x + 2)^2/4 "d"x`
= `pi/4 [(x + 2)^3/3]_0^2`
= `pi/4 [64/3 - 8/3]`
= `pi/4[56/3]`
= `14/3 pi "m"^3`
Volume of the frustum = `14/3 pi "m"^3`
APPEARS IN
RELATED QUESTIONS
Find by integration, the volume of the solid generated by revolving about the x-axis, the region enclosed by y = 2x2, y = 0 and x = 1
Find, by integration, the volume of the solid generated by revolving about the x axis, the region enclosed by y = e-2x, y = 0, x = 0 and x = 1
Find, by integration, the volume of the solid generated by revolving about the y axis, the region enclosed by x2 = 1 + y and y = 3
The region enclosed between the graphs of y = x and y = x2 is denoted by R. Find the volume generated when R is rotated through 360° about x-axis
A watermelon has an ellipsoid shape which can be obtained by revolving an ellipse with major-axis 20 cm and minor-axis 10 cm about its major-axis. Find its volume using integration
Choose the correct alternative:
The volume of solid of revolution of the region bounded by y2 = x(a – x) about the x-axis is
