Question

Find the equation of a curve passing through the point (0, 2), given that the sum of the coordinates of any point on the curve exceeds the slope of the tangent to the curve at that point by 5.

Answer 1

Since, dy/dx represents the slope of tangent to a given curve at a point (x, y), the given equation is

dy/dx+5=x+y

`therefore dy/dx-y=(x-5)`

The given equation is of the form dy/dx+Py=Q

where,P=-1 and Q=(x-5)

`therefore I.F=e^(intPdx)=e^(int-1dx)=e^-x`

∴ Solution of the given equation is

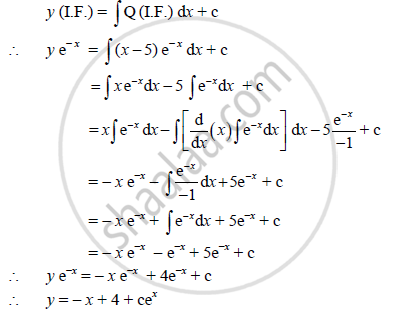
∴ x + y - 4 = cex is the general solution.
Since the curve is passing through the point (0, 2)

∴ x = 0, y = 2
∴ 0 + 2 - 4 = ce0
∴ c = - 2
∴ x + y - 4 = - 2e^x

y = 4 - x - 2e^x is the required equation of the curve.