Advertisements
Advertisements
Question
Find out the increase in moment of inertia I of a uniform rod (coefficient of linear expansion α) about its perpendicular bisector when its temperature is slightly increased by ∆T.
Solution
Let the mass and length of a uniform rod be M and l respectively.
Moment of inertia of the rod about its perpendicular bisector. `(i) = (Ml^2)/12`
The increase in length of the rod when temperature is increased by ∆T is given by `∆l = l.α∆T` .....(i)
∴ New moment of inertia of the rod `(I) = M/12 (l + ∆l)^2`
= `M/12 (l^2 + ∆l^2 + 2I∆l)`
As the change in length ∆l is very small, therefore, neglecting `(∆l)^2`, we get
`I^' = M/12 (l^2 + 2l∆l)`
= `(Ml^2)/12 + (MI∆l)/6`
= `l + (MI∆l)/6`
∴ Increase in the moment of inertia `∆I = l - I`
= `(MI∆l)/6`
= `2 xx ((Ml^2)/12) (∆l)/l`
`∆I = 2*I α∆T` ......[Using equation (i)]
APPEARS IN
RELATED QUESTIONS
Is it possible for two bodies to be in thermal equilibrium if they are not in contact?
A system X is neither in thermal equilibrium with Y nor with Z. The systems Y and Z
Solve the following problem.
A blacksmith fixes iron ring on the rim of the wooden wheel of a bullock cart. The diameter of the wooden rim and the iron ring are 1.5 m and 1.47 m respectively at room temperature of 27 °C. To what temperature the iron ring should be heated so that it can fit the rim of the wheel? (αiron = 1.2 × 10–5K–1).
A metre scale made of a metal reads accurately at 25 °C. Suppose in an experiment an accuracy of 0.12 mm in 1 m is required, the range of temperature in which the experiment can be performed with this metre scale is ______.(coefficient of linear expansion of the metal is `20 xx 10^-6 / (°"C")`
A metal rod is heated to t°C. A metal rod has length, area of cross-section, Young's modulus and coefficient of linear expansion as 'L', 'A', 'Y' and 'a' respectively. When the rod is heated, the work performed is ______.
A metal rod of length Land cross-sectional area A is heated through T °C. What is the force required to prevent the expansion of the rod lengthwise?
(Y = Young's modulus of material of the rod, α = coefficient of linear expansion of the rod.)
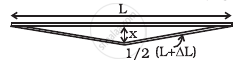
A rail track made of steel having length 10 m is clamped on a raillway line at its two ends (figure). On a summer day due to rise in temperature by 20° C, it is deformed as shown in figure. Find x (displacement of the centre) if αsteel = 1.2 × 10–5/°C.
Each side of a box made of metal sheet in cubic shape is 'a' at room temperature 'T', the coefficient of linear expansion of the metal sheet is 'α'. The metal sheet is heated uniformly, by a small temperature ΔT, so that its new temeprature is T + ΔT. Calculate the increase in the volume of the metal box.
Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
- Assertion A: When a rod lying freely is heated, no thermal stress is developed in it.
- Reason R: On heating, the length of the rod increases. In light of the above statements.
choose the correct answer from the options given below:
A metal rod Y = 2 × 1012 dyne cm-2 of coefficient of linear expansion 1.6 × 10-5 per °C has its temperature raised by 20°C. The linear compressive stress to prevent the expansion of the rod is ______.
