Advertisements
Advertisements
Question
Find the ratio in which the y-axis divides the line segment joining the points (−4, − 6) and (10, 12). Also find the coordinates of the point of division ?
Solution
Let the y-axis divide the line segment joining the points (−4, −6) and (10, 12) in the ratio λ : 1. and the point of the intersection be (0, y).
So, by section formula, we have:
`((10lambda+(-4))/(lambda+1),(12lambda+(-6))/(lambda+1))=(0,y)`
`therefore(10lambda+(-4))/(lambda+1)=0rArr10lambda-4=0`
`rArrlambda=4/10=2/5`
`thereforey=(12lambda+(-6))/(lambda+1)=(12xx2/5-6)/(2/5+1)=((24-30/5))/((2+5)/5)`
Thus, the y-axis divides the line segment joining the given points in the ratio 2 : 5 and the point of division is`(0,-6/7)`
APPEARS IN
RELATED QUESTIONS
Find the ratio in which y-axis divides the line segment joining the points A(5, –6) and B(–1, –4). Also find the coordinates of the point of division.
Find the ratio in which the line segment joining A (1, −5) and B (−4, 5) is divided by the x-axis. Also, find the coordinates of the point of division.
A point P divides the line segment joining the points A(3, -5) and B(-4, 8) such that `(AP)/(PB) = k/1`. If P lies on the line x + y = 0, then find the value of k.
In the given figure, line APB meets the x-axis at point A and y-axis at point B. P is the point (−4, 2) and AP : PB = 1 : 2. Find the co-ordinates of A and B.
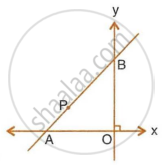
Find the coordinate of a point P which divides the line segment joining :
5(2, 6) and R(9, -8) in the ratio 3: 4.
Q is a point on the line segment AB. The coordinates of A and B are (2, 7) and (7, 12) along the line AB so that AQ = 4BQ. Find the coordinates of Q.
A (30, 20) and B ( 6, -4) are two fixed points. Find the coordinates of a point Pin AB such that 2PB = AP. Also, find the coordinates of some other point Qin AB such that AB = 6 AQ.
The point which divides the line segment joining the points (7, –6) and (3, 4) in ratio 1 : 2 internally lies in the ______.
The points A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC. Find the coordinates of the point P on AD such that AP : PD = 2 : 1
If (2, 4) is the mid-point of the line segment joining (6, 3) and (a, 5), then the value of a is ______.
