Advertisements
Advertisements
Question
Find the roots of the quadratic equations 2x2 – 7x + 3 = 0 by applying the quadratic formula.
Solution
2x2 – 7x + 3 = 0
On comparing this equation with ax2 + bx + c = 0, we get
a = 2, b = -7 and c = 3
By using quadratic formula, we get
`x = -b±sqrt(b2 - 4ac)/(2a)`
`⇒ x = 7±sqrt(49 - 24)/4`
`⇒ x = 7±sqrt25/4`
`⇒ x = 7±5/4`
`⇒ x = (7+5)/4 `
`⇒ x = 12/4 " or " 2/4`
`∴ x = 3 " or " 1/2`
APPEARS IN
RELATED QUESTIONS
Solve the following quadratic equation by completing square method : x2 + 10x + 21 = 0.
Find the roots of the following quadratic equations, if they exist, by the method of completing the square 2x2 + x – 4 = 0
`3x^2-2x-1=0`
`4x^2+4bx-(a^2-b^2)=0`
By using the method of completing the square, show that the equation `2x^2+x+4=0` has no real roots.
The length of a rectangle is thrice as long as the side of a square. The side of the square is 4 cm more than the width of the rectangle. Their areas being equal, find the dimensions.
Solve the following quadratic equation by completing the square method.
5x2 = 4x + 7
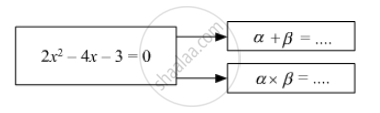
Fill in the gaps and complete.
If α, β are roots of quadratic equation,
The value of \[\sqrt{6 + \sqrt{6 + \sqrt{6 +}}} . . . .\] is
The positive root of `sqrt(3"x"^2 + 6)` = 9 is:
