Question

Find the shortest distance between the lines

`(x+1)/7 = (y + 1)/(-6) = (z + 1)/1 and (x - 3)/1 = (y - 5)/(-2) = (z - 7)/1`

Answer 1

Shortest distance between the lines

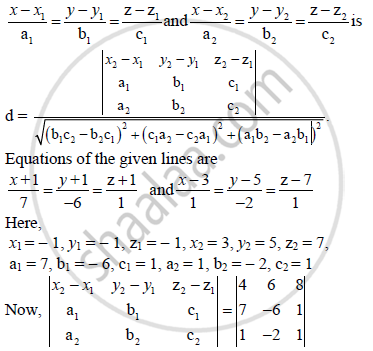
= 4(−6 + 2) − 6(7 − 1) + 8(−14 + 6)

= − 16 − 36 − 64

= − 116

and `(b_1c_2 - b_2c_1)^2 + (c_1a_2 - c_2a_1)^2 + (a_1b_2 - a_2b_1)^2`

= (−6 + 2)2 + (1 − 7)2 + (−14 + 6)2

= 16 + 36 + 64

= 116

∴ shortest distance between the given lines

`|(-116)/sqrt(116)|`

`sqrt(116)`

= `2sqrt(29)` units