Advertisements
Advertisements
Question
Find the smallest number by which 28812 must be divided so that the quotient becomes a perfect square.
Solution
Prime factorisation of 28812:
28812 = 2 x 2 x 3 x 7 x 7 x 7 x 7
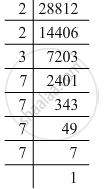
Grouping them into pairs of equal factors:
28812 = (2 x 2) x (7 x 7) x (7 x 7) x 3
The factor, 3 is not paired. Hence, the smallest number by which 28812 must be divided such that the resulting number is a perfect square is 3.
APPEARS IN
RELATED QUESTIONS
Which of the following numbers are perfect square?
11
Which of the following numbers are perfect square?
12
Which of the following numbers are perfect square?
32
Which of the following numbers are perfect square?
111
Using prime factorization method, find which of the following numbers are perfect square?
441
Using prime factorization method, find which of the following numbers are perfect square?
343
By what number should each of the following numbers be multiplied to get a perfect square? Also, find the number whose square is the new number.
2880
By what numbers should each of the following be divided to get a perfect square ? Also, find the number whose square is the new number.
1575
Find the smallest number by which 4851 must be multiplied so that the product becomes a perfect suqare.
The following number are not perfect squares. Give reason.
1547
