Advertisements
Advertisements
Question
Find the squares of the following numbers using diagonal method:
171
Solution
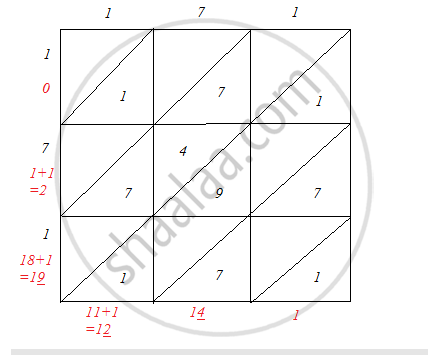
\[\therefore\] 1712 = 29241
APPEARS IN
RELATED QUESTIONS
Write a Pythagorean triplet whose one member is 18.
What will be the units digit of the square of the following number?
4583
What will be the units digit of the square of the following number?
55555
Which of the following triplets are pythagorean?
(8, 15, 17)
Which of the following triplet is pythagorean?
(18, 80, 82)
Which of the following triplet pythagorean?
(16, 63, 65)
Observe the following pattern \[1 = \frac{1}{2}\left\{ 1 \times \left( 1 + 1 \right) \right\}\]
\[ 1 + 2 = \frac{1}{2}\left\{ 2 \times \left( 2 + 1 \right) \right\}\]
\[ 1 + 2 + 3 = \frac{1}{2}\left\{ 3 \times \left( 3 + 1 \right) \right\}\]
\[1 + 2 + 3 + 4 = \frac{1}{2}\left\{ 4 \times \left( 4 + 1 \right) \right\}\]and find the values of following:
31 + 32 + ... + 50
Observe the following pattern \[1^2 = \frac{1}{6}\left[ 1 \times \left( 1 + 1 \right) \times \left( 2 \times 1 + 1 \right) \right]\]
\[ 1^2 + 2^2 = \frac{1}{6}\left[ 2 \times \left( 2 + 1 \right) \times \left( 2 \times 2 + 1 \right) \right]\]
\[ 1^2 + 2^2 + 3^2 = \frac{1}{6}\left[ 3 \times \left( 3 + 1 \right) \times \left( 2 \times 3 + 1 \right) \right]\]
\[ 1^2 + 2^2 + 3^2 + 4^2 = \frac{1}{6}\left[ 4 \times \left( 4 + 1 \right) \times \left( 2 \times 4 + 1 \right) \right]\] and find the values :
52 + 62 + 72 + 82 + 92 + 102 + 112 + 122
The hypotenuse of a right triangle with its legs of lengths 3x × 4x is ______.
Can a right triangle with sides 6 cm, 10 cm and 8 cm be formed? Give reason.
